The goal of the bate package is to present some
functions to compute quantiles of the empirical distribution of the
bias-adjusted treatment effect (BATE) in a linear econometric model with
omitted variables. To analyze such models, a researcher should consider
four regression models: (a) a short regression model where the outcome
variable is regressed on the treatment variable, with or without
additional controls; (b) an intermediate regression model where
additional control variables are added to the short regression; (c) a
hypothetical long regression model, where an index of the
omitted variable(s) is added to the intermediate regressions; and (d) an
auxiliary regression where the treatment variable is regressed on all
observed (and included) control variables.
As an example, suppose a researcher has estimated the following model, y = α + β1x + γ1w1 + γ2w2 + ε , and is interested in understanding the impact of some omitted variables on the results. In this case:
The treatment effect is β1, but in the presence of omitted variables, this will be estimated with a bias. The functions in this package will allow a researcher to create quantiles of the empirical distribution of the BATE, i.e. the treatment effect once we have adjusted for the effect of omitted variable bias.
The researcher will need to supply the data set (as a data frame), the name of the outcome variable, the name of the treatment variable, and the names of the additional regressors in the intermediate regression. The functions in this package will then compute the quantiles of the empirical distribution of BATE.
Two parameters capture the effect of the omitted variables in this set up.
The first parameter is δ. This captures the relative
strength of the unobservables, compared to the observable controls, in
explaining variation in the treatement variable. In the
functions below this is denoted as the parameter delta.
This parameter is a real number and can take any value on the real line,
i.e. it is unbounded. Hence, in any specific analysis, the researcher
will have to choose a lower and an upper bound for delta.
For instance, if in any empirical analysis, the researcher believes,
based on knowledge of the specific problem being investigated, that the
unobservables are less important than the observed controls in
explaining the variation in the treatment variable, then she
could choose delta to lie between 0 and 1. On the other
hand, if she believes that the unobservables are more important
than the observed controls in explaining the variation in the
treatment variable, then she should choose delta
to lie between 1 and 2 or 1 and 5.
The second parameter is
Rmax. This captures the
relative strength of the unobservables, compared to the observable
controls, in explaining variation in the outcome variable. In
the functions below, this is captured by the parameter
Rmax. The parameter Rmax is the R-squared in
the hypothetical long regression. Hence, it lies between the R-squared
in the intermediate regression (R̃) and 1. Since the lower bound
of Rmax is given by R̃, in any specific analysis,
the researcher will only have to choose an upper bound for
Rmax.
In a specific empirical analysis, a researcher will use domain
knowledge about the specific issue under investigation to determine a
plausible range for delta (e.g. 0.01 ≤ δ ≤ 0.99).
This will be given by the interval on the real line lying between
deltalow and deltahigh (the researcher will
choose deltalow and deltahigh). Using the
example in this paragraph, deltalow=0.01 and
deltahigh=0.99.
In a similar manner, a researcher will use domain knowledge about the
specific issue under investigation to determine Rmax. Here,
it will be important to keep in mind that Rmax is the
R-squared in the hypothetical long regression. Now, it is unlikely that
including all omitted variables and thereby estimating the hypothetical
long regression will give an R-squared of 1. This is because, even after
all the regressors have been included, some variation of the outcome
might be plausibly explained by a stochastic element. Hence,
Rmax will most likely be different from, and less than, 1.
This will be denoted by Rhigh
(e.g. Rmax=0.61).
How is the omitted variable bias and the BATE computed? The key
result that is used to compute the BATE is this: the omitted variable
bias is the real root of a cubic equation whose coefficients
are functions of the parameters of the short, intermediate and auxiliary
regressions and the values of delta and Rmax.
In a specific empirical analysis, the parameters of the short,
intermediate and auxiliary regressions are known. Hence, the
coefficients of the cubic equation become functions of
delta and Rmax, the two key parameters that
the researcher chooses, using domain knowledge.
Once the researchers has chosen deltalow,
deltahigh and Rhigh, this defines a bounded
box on the (delta, Rmax) plane defined by the
Cartesian product of the interval [deltalow,
deltahigh] and of the interval [Rlow,
Rhigh]. The main functions in this package computes the
root of the cubic equation on a sufficiently granular grid (the degree
of granularity will be chosen by the user) covering the bounded box.
To compute the root of the cubic equation, the algorithm first evaluates the discriminant of the cubic equation on each point of the grid and partitions the box into two regions: (a) unique real root (URR) and NURR (no unique real root). There are three cases to consider.
delta direction to generate a nonempty intersection
with a URR region. Once that is found, the algorithm implements the
steps outlined in step 2.The bias is then used to compute the BATE, which is defined as the estimated treatment effect in the intermediate regression minus the bias. This will generate an empirical distribution of the BATE. Asymptotic theory shows that the BATE converges in probability to the true treatment effect. Hence, the interval defined by the 2.5-th and 97.5-th quantiles of the empirical distribution of the BATE will contain the true treatment effect with 95 percent probability.
An useful function to collect relevant parameters from the short, intermediate and auxiliary regressions is:
collect_par(): collects parameters from the short,
intermediate and auxiliary regressions; (user provides name of the data
set, name of outcome variable, name of treatment variable, names of
control variables in the short regression, if relevant, and names of
additional variables in the intermediate regression); the output of this
function is a data frame.Users can use the output from collect_par() to construct
an area plot of the bounded box using:
urrplot(): creates a colored area plot of the bounded
box chosen by the user demarcating the area where the cubic equation has
unique real root (URR) from the area where the cubic equation has three
real roots (NURR); the output is a plot object.The main functions in this package that are available for users to compute empirical distributions of omitted variable bias and BATE are:
ovbias(): computes the empirical distribution of
omitted variable bias and BATE (takes the output from
collect_par() as one of the inputs); the output of this
function is a list;ovbias_par(): computes the empirical distribution of
omitted variable bias and BATE (takes the data frame, name of outcome
variable, name of treatment variable, names of control variables in the
short regression, if relevant, and names of additional variables in the
intermediate regression, as inputs); the output of this function is a
list;ovbias_lm(): computes the empirical distribution of
omitted variable bias and BATE (takes three lm objects
corresponding to the short, intermediate and auxiliary regressions as
inputs); the output of this function is a list.Using the output from ovbias(),
ovbias_par() or ovbias_lm(), users can
construct various plots:
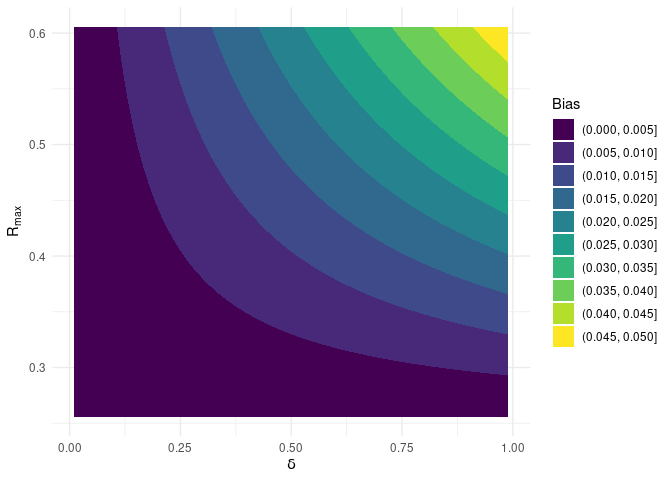
cplotbias(): contour plot of the bias over the bounded
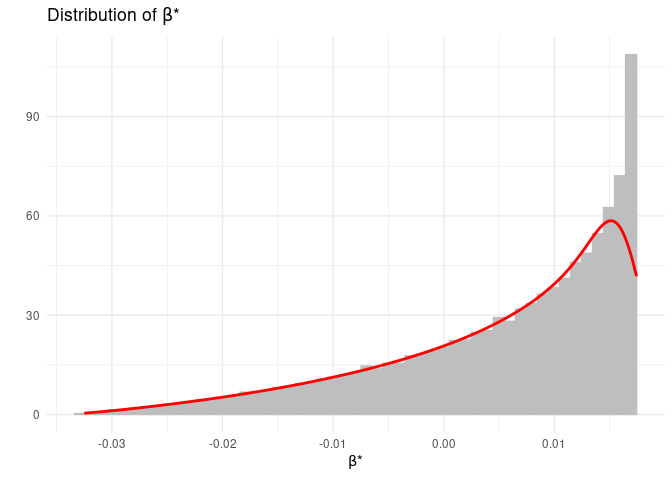
box; the output of this function is a plot object;dplotbate(): histogram and density plot of BATE; the
output of this function is a plot object;The methodology proposed in Oster (2019) is implemented via these functions:
osterbds(): identified sets according to Oster’s
methodology; the output of this function is a data frame;osterdelstar(): the value of δ* for
a chosen value of Rmax;
the output of this function is a data frame;delfplot(): a plot of the graph of the function,
δ = f(Rmax);
the output of this function is a plot object.You can install the development version of bate from GitHub with:
# install.packages("devtools")
devtools::install_github("dbasu-umass/bate")Let us load the data set.
data("NLSY_IQ")The data set has two .RData objects:
NLSY_IQ (to be used for the analysis of maternal behavior
on child IQ) and NLSY_BW (to be used for the analysis of
maternal behavior on child birthweight).
Let us see the names of the variables in the NLSY_IQ
data set.
names(NLSY_IQ)
#> [1] "iq_std" "BF_months" "mom_drink_preg_all"
#> [4] "lbw_preterm" "age" "female"
#> [7] "black" "motherAge" "motherEDU"
#> [10] "mom_married" "income" "sex"
#> [13] "race"Let us set age and race as factor
variables
NLSY_IQ$age <- factor(NLSY_IQ$age)
NLSY_IQ$race <- factor(NLSY_IQ$race)Let us work with the following example:
iq_std ~ BF_months + sex + ageiq_std ~ BF_months + sex + age + income + motherAge + motherEDU + mom_married + race.Let us use the collect_par() function to collect
parameters from the short, intermediate and auxiliary regressions. Note
how other_parameters is a subset of control.
The researcher needs to make sure that control includes the
names of all regressors in the intermediate regression, other
than the treatment variable.
parameters <- bate::collect_par(data=NLSY_IQ,
outcome="iq_std",
treatment="BF_months",
control=c("age","sex","income","motherAge","motherEDU","mom_married","race"),
other_regressors = c("sex","age"))Let us see the parameters.
(parameters)
#> beta0 R0 betatilde Rtilde sigmay sigmax taux
#> BF_months 0.04447926 0.04465201 0.01740748 0.255621 0.9900242 4.629618 18.99883Let us choose the dimensions of the bounded box over which we want the bias computation to be carried out.
# Upper bound of Rmax
Rhigh <- 0.61
# Lower bound of delta
deltalow <- 0.01
# Upper bound of delta
deltahigh <- 0.99
# step size to construct grid
e <- 0.01Now we can use the ovbias() function to compute the
empirical distribution of omitted variable bias and BATE. Note that this
step make take a few minutes, depending on the dimensions of the box and
the size of e, to complete itself.
OVB <- bate::ovbias(
parameters = parameters,
deltalow=deltalow,
deltahigh=deltahigh,
Rhigh=Rhigh,
e=e)We can now see the quantiles of omitted variable bias
(OVB$bias_Distribution)
#> 2.5% 5% 50% 95% 97.5%
#> 0.000 0.000 0.009 0.034 0.039and quantiles of the BATE (computed over the bounded box we chose above).
(OVB$bstar_Distribution)
#> 2.5% 5% 50% 95% 97.5%
#> -0.021 -0.017 0.009 0.017 0.017We can create the histogram and density plot of the omitted variable bias.
bate::dplotbate(OVB$Data)
We can also create a contour plot of BATE over the bounded box.
bate::cplotbias(OVB$Data)