

Joint variable importance plot (jointVIP) visualizes each variable’s outcome importance via Pearson’s correlation and treatment importance via cross-sample standardized mean differences. Bias curves enable comparisons to support variable prioritization among potential confounders.
You can install the jointVIP package on CRAN using:
# for version on CRAN
install.packages("jointVIP")
# for development version on github
devtools::install_github("ldliao/jointVIP")To demonstrate, we use the 2015 Behavioral Risk Factor Surveillance
System (BRFSS) example to answer the causal question: Does smoking
increase the risk of chronic obstructive pulmonary disease (COPD)? The
data and background is inspired by Clay
Ford’s work from University of Virginia Library. First, the data is
cleaned to only have numeric variables, i.e., all factored variables are
transformed via one-hot-encoding. Treatment variable smoke
only contains 0 (control) and 1 (treatment).
With the cleaned data, you can specify details in the function
create_jointVIP() like so:
library(jointVIP)
## basic example code
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following object is masked from 'package:testthat':
#>
#> matches
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
# load data
data('brfss', package='jointVIP')
treatment = 'smoke'
outcome = 'COPD'
covariates = names(brfss)[!names(brfss) %in% c(treatment, outcome)]
## select the pilot sample from random portion
## pilot data here are considered as 'external controls'
## can be a separate dataset; should be chosen with caution
set.seed(1234895)
pilot_prop = 0.2
pilot_sample_num = sample(which(brfss %>% pull(treatment) == 0),
length(which(brfss %>% pull(treatment) == 0)) *
## set up pilot and analysis data
## we want to make sure these two data are non-overlapping
pilot_df = brfss[pilot_sample_num, ]
analysis_df = brfss[-pilot_sample_num, ]
## minimal example
brfss_jointVIP = create_jointVIP(treatment = treatment,
outcome = outcome,
covariates = covariates,
pilot_df = pilot_df,
analysis_df = analysis_df)Generic functions can be used for the jointVIP object to
extract information as a glance with summary() and
print().
summary(brfss_jointVIP)
#> Max absolute bias is 0.032
#> 3 variables are above the desired 0.01 absolute bias tolerance
#> 13 variables can be plottedprint(brfss_jointVIP)
#> bias
#> age_over65 0.032
#> average_drinks 0.031
#> age_25to34 0.012plot(brfss_jointVIP)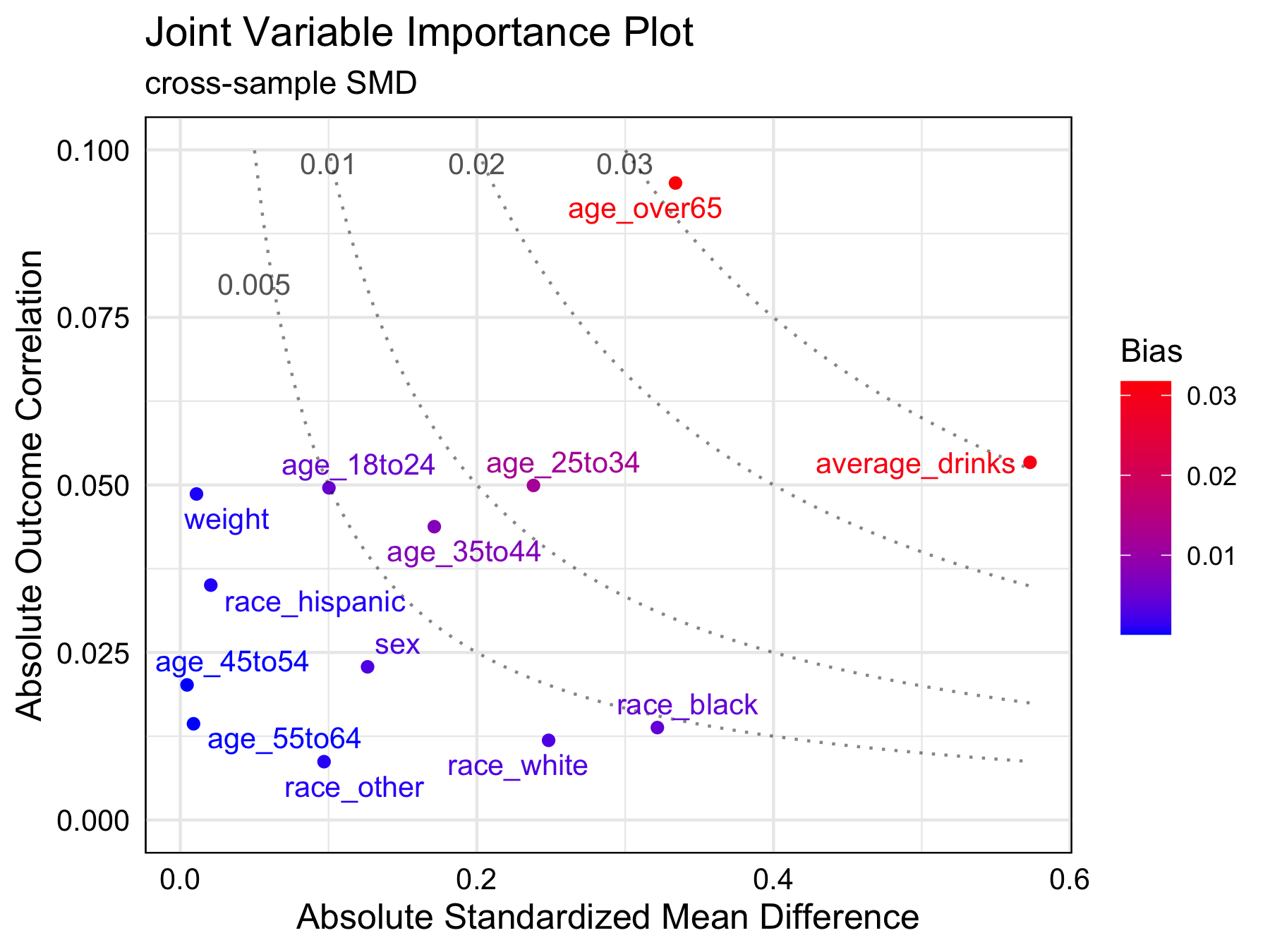
In this example, age_over65 and
average_drinks are two most important variables to adjust.
At a bias tolerance of 0.01, 3 variables: age_over65,
average_drinks, and age_25to34 are above the
tolerance threshold. Moreover, age_over65 and
average_drinks are of higher importance for adjustment than
age_25to34. Although race_black and
age_over65 have similar absolute standardized mean
differences (0.322 and 0.333, respectively), age_over65 is
more important to adjust for since its highly correlated with the
outcome.