The package slasso implements the smooth LASSO
estimator (S-LASSO) for the Function-on-Function linear regression model
proposed by Centofanti et al. (2022). The S-LASSO estimator is able to
increase the interpretability of the model, by better locating regions
where the coefficient function is zero, and to smoothly estimate
non-zero values of the coefficient function. The sparsity of the
estimator is ensured by a functional LASSO penalty, which pointwise
shrinks toward zero the coefficient function, while the smoothness is
provided by two roughness penalties that penalize the curvature of the
final estimator. The package comprises two main functions
slasso.fr and slasso.fr_cv. The former
implements the S-LASSO estimator for fixed tuning parameters of the
smoothness penalties \(\lambda_s\) and
\(\lambda_t\), and tuning parameter of
the functional LASSO penalty \(\lambda_L\). The latter executes the K-fold
cross-validation procedure described in Centofanti et al. (2022) to
choose \(\lambda_L\), \(\lambda_s\), and \(\lambda_t\).
The development version can be installed from GitHub with:
# install.packages("devtools")
devtools::install_github("unina-sfere/slasso")This is a basic example which shows you how to apply the two main
functions slasso.fr and slasso.fr_cv on a
synthetic dataset generated as described in the simulation study of
Centofanti et al. (2022).
We start by loading and attaching the slasso package.
library(slasso)Then, we generate the synthetic dataset and build the basis function sets as follows.
data<-simulate_data("Scenario II",n_obs=500)
X_fd=data$X_fd
Y_fd=data$Y_fd
domain=c(0,1)
n_basis_s<-30
n_basis_t<-30
breaks_s<-seq(0,1,length.out = (n_basis_s-2))
breaks_t<-seq(0,1,length.out = (n_basis_t-2))
basis_s <- fda::create.bspline.basis(domain,breaks=breaks_s)
basis_t <- fda::create.bspline.basis(domain,breaks=breaks_t)To apply slasso.fr_cv, sequences of \(\lambda_L\), \(\lambda_s\), and \(\lambda_t\) should be defined.
lambda_L_vec=10^seq(0,1,by=0.1)
lambda_s_vec=10^seq(-6,-5)
lambda_t_vec=10^seq(-5,-5) And, then, slasso.fr_cv is executed.
mod_slasso_cv<-slasso.fr_cv(Y_fd = Y_fd,X_fd=X_fd,basis_s=basis_s,basis_t=basis_t,
lambda_L_vec = lambda_L_vec,lambda_s_vec = lambda_s_vec,lambda_t_vec =lambda_t_vec,
max_iterations=1000,K=10,invisible=1,ncores=12)The results are plotted.
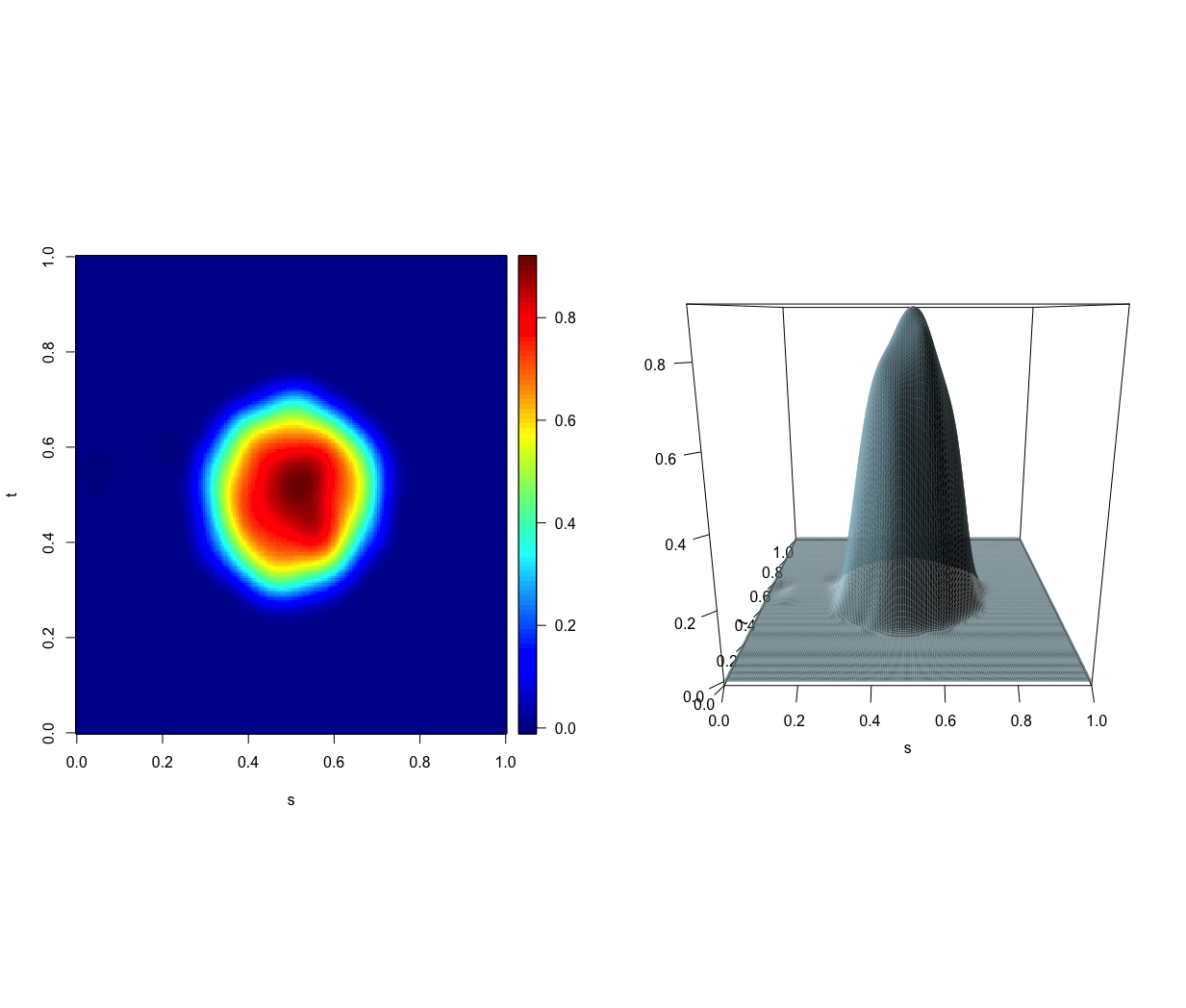
plot(mod_slasso_cv) By using the
model selection method described in Centofanti et al. (2022), the
optimal values of \(\lambda_L\), \(\lambda_s\), and \(\lambda_t\), are \(3.98\), \(10^{-5}\), and \(10^{-5}\), respectively.
By using the
model selection method described in Centofanti et al. (2022), the
optimal values of \(\lambda_L\), \(\lambda_s\), and \(\lambda_t\), are \(3.98\), \(10^{-5}\), and \(10^{-5}\), respectively.
Finally, sasfclust is applied with \(\lambda_L\), \(\lambda_s\), and \(\lambda_t\) fixed to their optimal
values.
mod_slasso<-slasso.fr(Y_fd = Y_fd,X_fd=X_fd,basis_s=basis_s,basis_t=basis_t,
lambda_L = mod_slasso_cv$lambda_opt_vec[1],lambda_s = mod_slasso_cv$lambda_opt_vec[2],
lambda_t = mod_slasso_cv$lambda_opt_vec[3],invisible=1,max_iterations=1000)The resulting estimator is plotted as follows.
plot(mod_slasso)